 |
| 標準スプリング |
| ★圧縮バネ |
| 中型(SWP-A) |
| 小型(SUS304) |
| ★引張バネ |
| 中型1(SWP-A) |
| 中型2(SWP-A) |
| 小型1(SUS304) |
| 小型2(SUS304) |
| 注文・お問合せ |
| 各種精密機械加工 |
| kpring製品案内 |
1)開発の主旨
2)開発経過
3)Soft-King-1の機能と適用機種
4)適用機種名
5)線材コイルばね(圧縮、引張)の設計要素
6)規格化の目的と必要性
7)PD方式による規格化
Ⅱ.『ケプリング』について
1)特 徴
Ⅱ.『ケプリング』について
a)求める製品の選択が容易
ばね定数をパラメータとして整理されているので、必要な性能(ばね定数)をもつばねを選び易い。
b)安心して使える強度
ばねの許容応力は各線材のもつ、引張強さ(σβ)に対して一定の割合のもとに定めており、常に荷重に対して最大応力値を知ることが出来ます。
従って、疲れ強度を推定し易い。
c)豊富な製造実績を反映
コンピュータを駆使して、約数10万点のばねを理論的に計算させ、その中から使用及び製造上の諸条件を考慮して定められた製品を選ぶことができます。
d)JIS(日本工業規格)に基づく設計
従来の理論を積み上げ、整理したものなので、あらゆる製品の規格化と連動し、ばね製品の国際規格の起点となることが期待されます。
e)高品質、高精度
吟味された材料、治工具、機械等卓越した生産技術と徹底した品質管理下での生産により、特に精度と品質の向上を企図しています。
以上述べたように、『ケプリング』は只単に形状だけの規格化ではなく、あらゆる用途に摘要出来る様に、ばねの性能別に整理され、理論的にも十分な検討を加え規格化を図った点が最大の特徴となっています。
ケプリングは、各ユーザーの立場から、諸条件を十分勘案して合理的に広い範囲の使用を充足させる製品といたしました。
次の手順によって、最適な製品を選ぶことが出来ます。
特にばねの性能である、ばね定数Kをパラメータにして整理されているのでまず求めるばねのばね定数Kを知る必要があります。
尚、ばね定数Kの値が直ちに知られている時は直接 iv)へ進んで下さい。
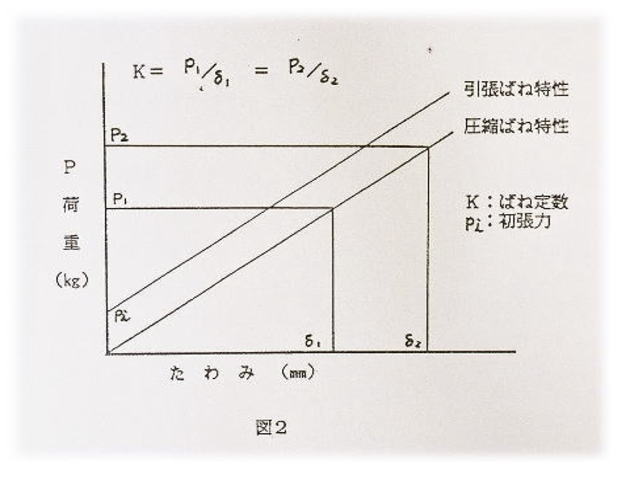
a)必要とする荷重Pを定める。
常用荷重・・・・・・・・・・・・・ P1(㎏)
又は、最大荷重・・・・・・・・・・・・・ P2(㎏) (P1=0.8×P2)
b)必要とするたわみ(ひずみ量)δを定める。
P1の時のたわみ量・・・・ δ1(㎜)
又は、P2の時のたわみ量・・・・ δ2(㎜)
c)近似ばね定数Kを計算により求める。
K= P1/δ1 = P2/δ2 (㎏/㎜)
注)ばね定数とは、たわみ1㎜当たりの荷重の変化量をあらわす。
(ばね定数Kと後述のPD係数表のKM.K0.K1.K2.K3.とは異なるので注意して下さい。)
d)規格品のばね定数Kを決める。
各ページ毎にKの値が明示されている、c)で算出されたKの値に最も近い値のあるページを参照して下さい。
注)JIS(日本工業規格)1級品、荷重精度 ± 5%
2級品、荷重精度 ±10%
e)次に性能の欄のたわみ量δ1、δ2が、ⅱ)の必要とするたわみ量δ1又はδ2より多少大きい値の行から製品を選びます。
f)固有振動のチェック
負荷の状況が、ばねの固有振動数及び高次振動数近づくと共振して破損の恐れが生ずるので、作動振動数とばねの固有振動数の関係をチェクします。
以上の手順により、性能、強度共に理論的に十分考慮された製品を選ぶことが出来ます。個々に時間を費やして設計した注文品よりも、あらゆる点で優れたものであります。
この規格は関係各分野で試みられ、殆ど不可能とされていたコイルばねの規格化を、新しいPD方式なる手法により、設計に携わっている方の声を反映し、コンピュータを駆使し、製造技術に対する長年のノウハウをもとに編んだものであります。(尚、PD方式については、「PD方式による簡易コイルばね設計法(解説)を参照して下さい。」
従前から、実用小型圧縮及び引張ばねについて、一部規格化されている製品もありますが、目下の所その規格品は、コイル径、線径をパラメータにしたものでばねの特性については、その結果としての表示であり、必要とするばねの特性、即ち“ばね定数”はランダムなものでありました。従ってこれを精度、強度が第一に要求される、実際の製品の設計段階で、組み入れることは殆ど出来ませんでした。
ここに示す、ケプリング(キングの略称とも呼ぶ)規格の作成においては、今まで不可能であった、理論値と作成条件を十分に加味したばねを設計するソフトSoft-King-1を活用する事により実現致しました。
尚、ここではJISB2704「圧縮、引張コイルばね設計基準解説」(以下JIS解説という)と重複する部分は省き、補足する形で記述してありますので、JIS解説と併せて御活用下さい。
a)摘要範囲
円形断面を有する線材コイル圧縮ばね及び引張ばね。
b)材料
「JIS解説」では広範囲に摘要出来るよう、ごく一般的な解説となっています。
“キング”では安定した特性があり、且つ、市場性、実績を考慮してピアノ線SWP-Aと、ばね用ステンレス鋼線SUS304-WPBの二種類の材料(JIS規格)に限定しました。
c)計算式
ケプリングではPD方式によって、コンピュータで計算してあります。
応力の取り方は、鉄道技術研究所報告NO-333 富田勝信先生 論文 (1962)に記されています通り、各線材のもつ引張強さ δBの値の一定割合を許容剪断応力値としました。
疲労強度は多くの諸因数の相乗的な条件で決まりますが、まず、最大剪断応力値を満たし、更に、規格化の効果である一貫生産かんりシステムを採用することにより充分な品質管理が出来ますので、一段と疲労強度に対する信頼性を増しました。
(i)横弾性係数G及び有効巻数
Gの値のとり方について、JIS解説を十分吟味し、検討を重ね、更にばねの製造実績から、JISF0503(船舶機関部コイルばね)に定められたGの値、即ち、線径によりGの値を多少変える方法を選びました。本件はJIS解説にあるように、Gの値は有効巻数と関わって計算結果に影響するため、どちらの影響か本質的に不明確な点があります。
しかしピアノ線の場合、伸線加工による加工硬化によって上記のGの値が変化するものと考えられ、広く現在迄採用されてきた方式としました。
又、ステンレス線材については、線材のもつ基本的な性質がピアノ線と異なり、伸線によってGが低くなるということが文献にもありましたので、JIS解説での改正値G-7000(㎏/㎜2)をすべての線径に採用しました。
有効巻数については、JIS解説に、「ばねの特性を合わせる為に、有効巻数に適当な修正を加える必要がある。」と記述されていますが、加工時には当然かなりのスプリングバックがあり、熱処理時にも又、変形を起こし、巻数が変化します。従って、微妙なばね特性を有効巻数で調整することは至難の業であり特に巻数の多い場合はその管理は不可能といえます。又、次の理由から有効巻数に端数を出すことは避けました。
圧縮ばねの両座部分の形状は、理想的な研削で約3/4の部分が平らになり、残り1/4は研削されないので上下共座部に接触せず、この部分の両端の相対的な位置関係で座屈を起こし易くなります。そして、全巻数が整数値の時、最も安定した状態となります。
従って、キング規格では圧縮ばねの有効巻数は整数値とし、コイル径Dを多少修正することにより、特性を合わせることにしました。一般に計算時にはコイル中心径の値を用いますが、実際の外径にはこれに線径分を加える必要があり、線径は端数の付いた数字なので、いずれにしても、外径を整数値とすることは、困難であるからです。
引張ばねの有効巻数はJIS解説に記述してあるように、「1コイルをフックした時、0.5巻の有効巻数が、フック一つについて付加された」として計算してあります。
(ⅱ)応力修正係数
JIS解説と同じ Wahl の式を用いています。
(ⅲ)ばね定数 及び ばね指数
ばね定数(K)の値は、ばねのたわみ量が1㎜変化した時、荷重の変化量を表す値で、ばね固有の特性を表す大切な値です。
現在まで、この値を整理して設計をされることは無かったので、当然製品の種類も無制限になっています。
標準化に当たってはこの値を整理する必要があります。Kの値が出来るだけ細分化した規格値とすることは理想ですが、製品の種類を多くすることは標準化のメリットが薄れてしまいます。
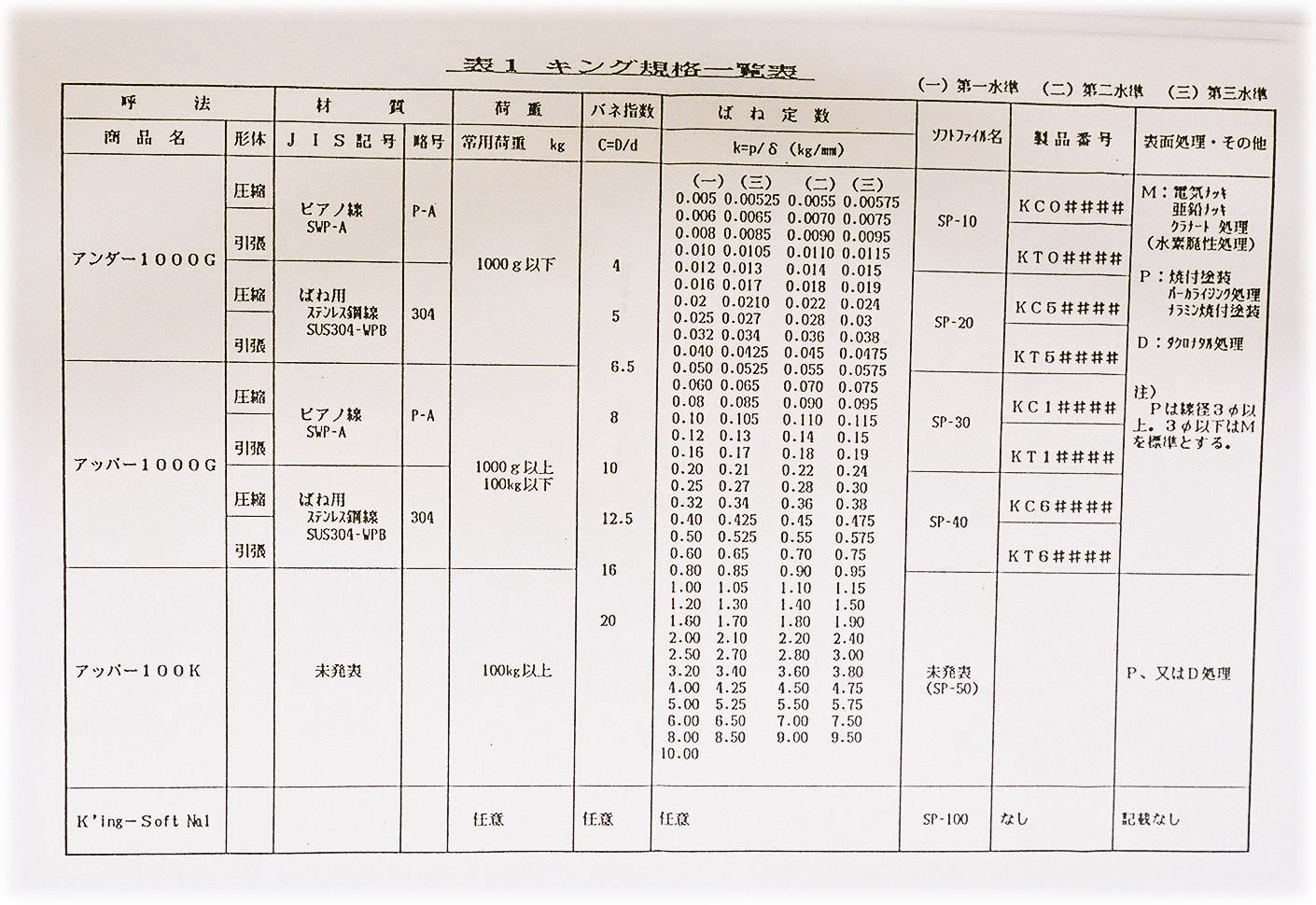
キング規格では、付表に示すように、JISZ8601標準数列を基礎に定めたもので、R10列を第一水準、R20列を第二水準、R40列を第三水準としてあります。
第一水準は、公比が約1.26の等比数列のKの値(10 0 . 1 ≒1.259)
第二水準は、公比が約1.12の等比数列のKの値(10 0.05≒1.259)
第三水準は、工比が約1.06の等比数列のKの値(100.025≒1.259)尚、ばねの精度については、JIS規格の1級品で±5%の許容差があり、一般には±10%程です。従って、価格、及び納期の点からも出来るだけ第一水準の規格品を選定されることが望ましい所です。
ばね指数(C=D/d)は、ばね定数が同一の時は形状とたわみ量を選ぶ値となります。
例えば、外径を小さくしたい時はCの値の小さい細長型、高さを低くしたい時はCの値の大きい巾広型を選びます。又、たわみ量はCの値が大きい程大きく取れるので、実際に必要なたわみ量からサイズを決めることになります。今迄の実績からみて、一般に小型のばねの場合、Cの値が多少大きく8ぐらい、中型のばねでは6.5ぐらいが多く採用されています。
(ⅳ)縦横比
これはばねの高さとコイル径の比を表すもので、ばね座屈を防ぐ為にJIS解説では実験結果を記載しています。
キング規格では座屈とは関係なく内側に軸の通る場合、又は外側にパイプ状のカバーを設ける場合もあるので、縦横比にかかわりなく、すべての圧縮ばね製品に技術データとして、内径ガイド、外径ガイドの推奨値を示してあります。縦横比が6以上になる時は内径または外径にガイドが必要となります。
(ⅴ)密着高さ
キング規格では、密着高さ=線径×(有効巻数+2)となっています。理論的には密着高さ=線径×(有効巻数+1.5)となるところですが、線径断面はコイル状に加工すると微少ながら楕円形になり、密着高さを大きくする方へと変形します。
特に現在あるコイリングマシンでは、線径を送る送りローラを上下強く締めすぎるとこの現象が大きくなりますので、巻数の多い圧縮コイルばねでは注意する必要があります。
尚、キング規格では、ばねの組立て時或いは調整時に最大たわみを起こしても、その後の特性に影響を与えない様にばねの密着時を最大荷重時として計算してあり、その内部応力値はJISの許容応力値の80%となっています。通常の作動の時は最大荷重80%の値である常用荷重、又は常用たわみを限度として使用されなければなりません。
(ⅵ)引張コイルばねの初張力
新しい実験式は用いないという基本方針に基づき、「JIS解説」にあるτi=G/(100C)の経験式を採用して初張力を表示してあります。又、キングの規格表は製造過程に於いて初張力を調整することを原則としました。これは近年ますます、高い精度が要求されるうえで、初張力の調整なしでは高精度の確保が出来ないからです。
(ⅶ)サージング
今迄、ユーザーの図面の中にばねの共振を考慮した図面はほとんど見られませんでした。あらゆる方面で使われており、共振によって問題を起こすケースが当然考えられますので、技術データとして表示しました。尚、計算式はJIS表示の通りです。
d)コイル端部 及びフックの形状
引張ばねのフック部の形状は強度上最も理想的なUフックを採用しましたが、特にアンダー1000Gタイプの小物については、当面、細線を用いた冷間での自動成形のためJISに示されている逆丸フックを採用することもあり、その旨、ユーザーの承認を仰ぐことにしました。
Uフックはコスト的に問題があるものの強度上より信頼性のあるばね規格とするため、敢えてUフックを採用しました。
又、引張ばねの強度はフック部の強度に左右されることが多いのでJIS解説を尊重し、引張ばねの許容応力を圧縮ばねの場合の80%にとり、最大荷重及び常用荷重を求めました。
e)ばね特性、及び寸法
JISに記載されている特性の許容量は、必要最小限の値として理解した上で、規格化を図り、品質管理を徹底し、許容差を当面約3%以内にすることを目途とします。
f)設計応力のとり方
基本的な考え方はJISと全く同じです。許容応力値をコンピュータ時代に即応してデジタル化して記憶させ、線径毎に引張強さδBの値と明確に連動させました。
即ち、線径によって多少異なるものの、剪断応力の許容値は圧縮ばねでは、概ね
τa≒0.5×0.8×σB=0.4×σB (ピアノ線)
τa≒0.5×0.8×0.8×σB=0.32×σB (ステンレス線)
を最大荷重時の応力とし、更に80%値を常用荷重時の応力としてあります。
又、引張ばねに於いては、フック部の強度を考慮して、更に80%の値を採用してあります。従って引張ばねの最大荷重時の許容応力は
τa≒0.4×0.8×σB=0.32×σB (ピアノ線)
τa≒0.4×0.8×0.8×σB=0.256×σB (ステンレス線)
常用荷重時の許容応力は、圧縮ばねと同じ様に上記の80%の値を採用しています。
(ⅰ)静荷重の場合
ア)静荷重とは
静荷重とは、ばねの使用状態で荷重変動のほとんどないもので、繰り返し荷重があってもばねの生涯を通じて約1000回以下のものを指しています。
イ)静荷重に考慮すべき要素
静荷重に考慮すべき要素として、温度と腐食があります。使用温度限界についてはJISの規格値を参考にして下さい。
又、腐食防止としてはキング規格では、亜鉛メッキ、クロメート処理(水素脆性処理)及びφ3以上は、下地処理後「焼付塗装」と「ダクロメタル処理」の3通りを基準とし、詳細はその都度、各ユーザーと打ち合わせを行っております。
(ⅱ)繰り返し荷重の場合
ア)ばねの疲れ強さ
常用荷重時の許容剪断応力の値は、
ピアノ線 τa=0.32×σB
ステンレス線 τa=0.256×σBであり
片振り両振りの疲れ限度(τWO)をも充足しています。
引張ばねについては更に80%の値となっていますので問題はありません。
イ)疲れ強さに及ぼす諸因子
特にショットピーニングの影響については設計上誤解されている点が多分にありますので、特に大切な部分をJIS解説から抜粋しておきます。
即ち「ピーニングによって負荷応力振巾は増大できるが、最大応力を大きくすることはできない。」
時々、ショットピーニングによって最大応力を大きく採れるとする設計者が多々みうけられます。
『ケプリング』規格では、ショットピーニング無しを標準としました。
a)あらまし
b)特徴
c)理論式とPD係数表
d)PD方式によるばね設計例
a)あらまし
各種工業製品の高性能化と多品種少量化により、ばねのユーザーとメーカーにとって今日程、設計手法の合理的統一がもとめられている時はなかったと言えましょう。ばねを取り入れた製品は数多くあり、且つ、ばね性能が即、製品性能となり、ばね設計の良否が、製品の良否の判定に直接結びついているといっても過言ではありません。
コイルばねを設計するには、
A.性能を定める「ばね定数」の公式
B.強度をチェックする「応力算出」の公式
の両公式を充たすことが必要。
先ず、ばねの性能(ばね定数)を決めるには、
① 線径
② コイル径
③ 有効巻数
の三要素を定める必要があります。
又、ばねの使用条件によって、材質、寿命、強度も考慮しなければならないので、単純と思われるばねの設計も二公式、三変数の解を得なければならず、以外と煩雑なものです。このため現場では、設計者は多大な労力を費やして不特定なばねのサイズを決めています。
PD方式は、従来のA,B二つの公式と線材の規格とによって、コイルばねの簡易設計法を考え出したものです。各分野で多用され、新技術開発への余力を生み出す一助ともなれば幸甚であります。
b)特徴
従来は三変数を定めるため、特殊計算尺、ノモグラム、計算数表及び、図表計算機、サンプル比較などを利用してきました。いずれも、三変数のうち 一変数を設計者が仮定して定めていたもので、いくらコンピュータの計算能力が大であっても基本的な煩雑さは解決されませんでした。
PD方式は、各線材のもつ許容応力値を、ばね設計に必要な計数として整理し、設計の初期の段階で変数値である線径の選定が出来る方式です。
従って、
① 線径の許容応力値を越えた、コイルばねのサイズは算出さ
れない。
② 一回の手順でサイズを決めることが出来る。
(但し、修正係数を配慮する時は一部繰り返しが必要)
③ 荷重と応力の関係が常に明らかである。
(荷重と応力は比例する)
等の特徴を有し、統一した設計手法を可能とすると同時に、この方式によって円筒コイルばねの規格化への道を開くことが出来ました。
次に、従来方式とPD方式の設計手順をフローチャートで示します。
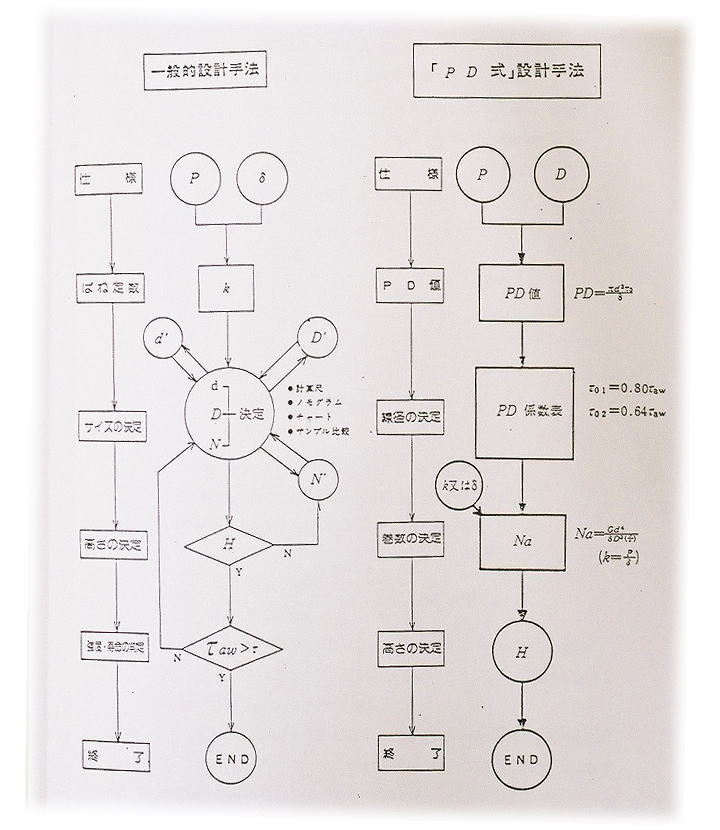
c)理論式とPD係数表
PD係数表とは、新しい理論式や実験式を用いたものではなく、フローチャートでお分かりのように、従来の応力の算式を下記の様に変形させ、各線径毎に固有の定数を算出して表にしたものです。通称、PD係数表といいます。
表 1.・・・・ピアノ線 SWP-A
表 2.・・・・ばね用ステンレス鋼線 SUS304-WPB
剪断応力の公式 τ=(8PD/πd3)・・・・・・・・(1)
ここで P:荷重
D:コイル中心径
d:線径
τ:剪断応力
(1)式を変形すると
PD=( τπd3/8)・・・・・・(2)
となる。
(2)式の右辺 τπd3/8は、線材によって定まる定数
(3)式の左辺PDは、設計時の仕様条件としてあたえられる。
(4)式でτを設計許容応力値( τn)に入れ換えて、
PD=τnπd3/8=Kn・・・・・・(3)
τn=0.8nτa ・・・・・・(4)
最大荷重時 τ0=τa PD=K0=τ0πd3/8
常用荷重時 τ1=0.8 τ0 PD=K1=τ1πd3/8
(5)式の定数を整理したものが、PD係数表です。(表1、表2)。
予め、各材質別、線径毎のPD計数値を用意することにより、PD≦Knの条件から、線径dを定めることが出来ます。
PD係数Knは寿命を考慮した、許容剪断応力値を引張強さδBと関連させて、段階的に決めて、(付表では80%を順次乗じて:鉄道技研究、富田勝信先生論文参照)
τ0 τ1 τ2・・・・・・を用いて、K0 K1 K2・・・・・・を算出しておくことにより疲労強度、腐食強度などを考慮し、あらゆる用途に段階的にこの方式を活用することが出来ます。
実際には前述した様にKの値は下表のようになります。
|
形状 |
設計荷重の状態 |
SWAP-A |
SUS304 |
||
|
設計許容せん断応力 |
Kn |
設計許容せん断応力 |
Kn |
||
|
圧縮ばね |
最 大 荷 重 常 用 荷 重 |
τ0≒0.4×σB τ1≒0.32×σB |
K0 K1 |
τ1≒0.32×σB τ2≒0.25×σB |
K1 K2 |
|
引張ばね |
最 大 荷 重 常 用 荷 重 |
τ1≒0.32×σB τ2≒0.256×σB |
K1 K2 |
τ2≒0.256×σB τ3≒0.2×σB |
K2 K3 |
d)PD方式によるばねの設計例
材質SWP-Aの場合
(1) D=37(㎜)・・・・・・・・・中心径
(2) P=8.5(㎏)・・・・・・・最大荷重
とすれば DP=314.5
PD係数表によりK1の項の(JIS許容応力の80%)の値でDP≦K1の値を充足する値345.92を得る。
その時線径は d=2.3(㎜)であり、横弾性係数は G=8200(㎏/㎜2)となります。
(3)最大たわみ、σ=77(㎜)とすれば
有効巻数
Na=Gd4δ/8D3P=Gd4/8D3K
=(8200×2.34/8×373)×(8.5/77)
=5.13
≒5
※ 精度を要する時は下記のようにDの値を少し変更することが望ましい。
(中心径Dの値は実際には内径、外径で定まるが、線径の値が小数点以下のものもあるので、有効巻数を制作上、及び座屈の関係より整数化してコイル径にて修正します。)
即ち、
D=(Gd4/8Nak)1/3
=(8200×2.34/8×5)×(8.5/77)1/3
=(51923.36)1/3
=37.3
密着高さ Hi=(Na+2)×d
=7×2.3=16.1
自由長さ H =16.1+77≒93
従って
中心径 37㎜ ・・・・・・(1)
最大荷重 8.5㎏ ・・・・・・(2)
最大たわみ 77㎜ ・・・・・・(3)
上記仕様のばねのサイズは
線径 2.3㎜
中心径 37.3㎜
有効巻数 5
自由長 93㎜
(尚、高さHは H≧Hi+δ として決めても理論上問題はないが、経験上(ピッチ)={(H-1.5d)/Na}<D/2の範囲としなければなりません。)
線径が決まれば、実際の応力は、
τ=(τa)×PD値/(K0)で求めることが出来ます。
従って上記仕様の実際の剪断応力は、表1矢印から
τa=90.50㎏/㎜2
K0=432.4
又、PD値は8.5(㎏)×37(㎜)から
PD=314.5
となるから
τ=90.50×314.5/432.4=65.8㎏/㎜2
となります。
引張ばねについてはPの値が初張力を含む値なので、同様の方法にて本表を使用することが出来ます。
尚、ステンレス材SUS304の時は別表、PD係数表、表2を用い同じ方法で設計して下さい。
文責 池田